File Example
What is an estimation problem?
The title of this course is "Observation theory: estimating the unknown". The three important ingredients are thus:
-
- observation: the measurements or observations that will be used;
- unknown: the parameter(s) that we are interested in;
- estimating: the link between the observations and the unknowns, this is the "estimation problem".
(Note that in this context 'estimation' is different from 'taking a wild guess' or the colloquial 'ballpark number'; it refers to a fundamental way to try to find the value for an unknown parameter, which is as close as possible to its true (but unknown) value.)
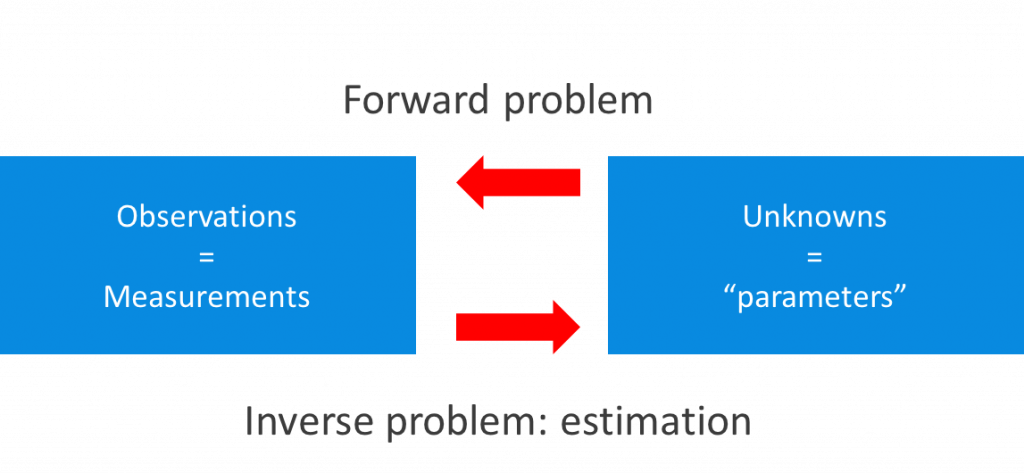
The relation between the observations and the unknowns can actually be viewed in two directions (see the figure above). If the correct values for the parameters would be known, and also their relation to the observations, this is called the forward problem: the corresponding "observations" can be determined exactly.
The estimation problem occurs in the other direction. This is the inverse problem: how to “determine” the unknown parameters, given a particular set of observations?
Since the inverse problem is notoriously difficult, it is not possible to determine, or calculate, the right answer. Estimation is the process to determine a possible solution for the unknown parameters, preferably as close to the true (but unknown) values as possible.

Linking and unlinking the mathematical model
In observation theory, we are trying to describe the 'real-world' by means of a mathematical model. In any such problem-solving process, one can recognize three consecutive stages:
-
- Linking the model: converting a real-world problem (described in common language) to a standardized mathematical model with well-defined observations and parameters
- Estimation, in which the mathematical model is used to estimate the parameters, in the idealized mathematical context;
- Unlinking the mathematical model: the estimated parameters (and their distributions) are converted back into the real world, interpreted, and assumed valid so that decisions can be made based on them.
This course focuses on stages 1 and 2: the aim is to estimate the unknown parameters of interest and to give an accompanying quality description. Stage 3 is usually very dependent on the specific situation at hand.
Uncertainty
In estimation problems, three types of uncertainty can be distinguished:
-
- Idealization due to the modelling: a mathematical model is an idealized and simplified version of the world around us. As such it can only result in an approximation of reality.
- Measurement errors: measurements are inherently subject to errors. This will be the topic of the next unit.
- Idealization in the measurement process: see below.
Idealization accuracy
Idealization refers to how well we can identify what we want to measure, and also how well we can really measure the points or quantities of interest. Examples:
-
- If we want to measure the width of a canal: how well can we depict the sides of the canal?
- If we want to map the corner of a house: how well can we identify and measure to the exact corner point?
The uncertainty due to the idealization means that additional errors are introduced - we will refer to this as idealization accuracy.